Two circles - Math Central

HOME

Math Central

Quandaries & Queries

Question from Luke, a student:

Two fixed circles intersect at A and B.
P is a variable point on one circle.
PA and PB when produced meet the other circle at M and N respectively.
Prove that MN is of constant length.
Thanks!

Here is the diagram that luke sent.

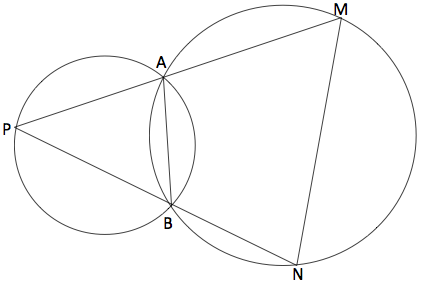
circles

Hi Luke,

You just have to put together three familiar circle theorems:

If O is the center of your circle ABNM and P is outside, then angle NPM = (1/2)(angle NOM - angle AOB).
If O is the center of your circle ABNM and P is inside, then angle NPM = (1/2)(angle NOM + angle AOB).
(Using neutral letters for this theorem because you will have to apply it to both your circles) if X,Y,and Z are three points on a circle whose center is C, then when X and C are on the same side of the line YZ, angle YXZ = (1/2) angle YCZ; when on opposite sides, angle YXZ + (1/2) angle YCZ = 180 degrees.

Chris

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.