| |||
| Math Central | Quandaries & Queries |
|
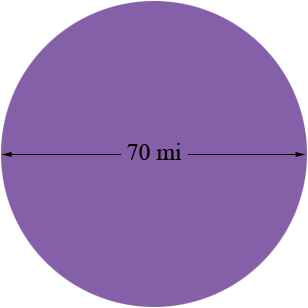
Question from Mable, a student: A circle that going 70mi across using 22/7 I need the area, radius, and the circumference |
Hi Mable,
There are a few things in mathematics that you really need to memorize. Some of these are properties of the circle. Your circle has a diameter of 70 miles. The radius of a circle is half the diameter so for your circle that's 35 miles.
The circumference of a circle is the distance around it. An amazing property of circles is that regardless of the size, if you divide the circumference of a circle by its diameter you always get the same answer. This number is given its own symbol, $\pi$, the Greek letter pi. Its value is approximately given by $3.1416$ and sometimes we use the approximate $\pi$ by $\frac{22}{7}$ although $3.1416$ is a better approximation.
Thus if a circle has circumference $c$ units and diameter $d$ units then $\large \frac{c}{d} = \pi.$ This is usually written $c = \pi d$ or if you are using the radius $r$ then $c = 2 \pi r.$ Use the approximation $\frac{22}{7}$ to approximate the circumference of your circle. Don't forget to include the units.
The formula for the area $A$ of a circle is $A = \pi r^2.$ Use the approximation $\frac{22}{7}$ to approximate the area of your circle. What are the units?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.