Hi Michael,

In my diagram I is the intersection, F is the position of the fast car and S is the position of the slow car at some time $t$ hours. The distances from the cars to the intersection and the distance between the cars are changing so $x, y$ and $z$ are functions of time, that is $x = x(t), y = y(t)$ and $z = z(t).$

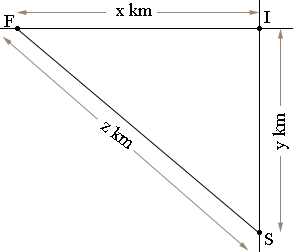
Since $IFS$ is a right triangle Pythagoras theorem gives us that

\[x(t)^2 + y(t)^2 = z(t)^2\]

Differentiate both sides of the equation with respect to $t$ to obtain an equation containing $x(t), x'(t), y(t), y'(t), z(t)$ and $z'(t).$ You know that $x'(t) = 70$ km/hr and $y'(t) = 40$ km/hr. Also at some particular time $t_0$ you know that $x(t_0) = 4$ km and $y(t_0) = 3$ km. What are $z(t_0)$ and $z'(t_0)?$

Penny