Hi Monty,

In my diagram $A$ is the center of the large circle and $B$ is the center of the small circle. The non-overlapped portion of the small circle is coloured yellow and its area is the area of the small circle, $\pi \; r^2 = \pi \; 3^2$ square inches, minus the sum of the areas of the regions shaded green and orange. I will show you how to find the area of half the orange region, the part above the line segment $DE$ and you can find the area of the region coloured green.

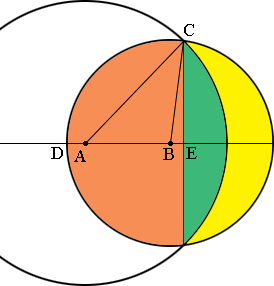
The part of the orange region above the line segment $DE$ is composed of the sector $BCD$ of the circle of radius 3 inches, and the right triangle $BEC.$ To calculate the area of the sector $BCD$ I need the measure of the angle $DBC.$ The lengths of the sides of the triangle $ABC$ are 3, 3.75 and 5 inches so I can use the Law of Cosines to determine the measure of the angle $ABC.$

\[5^2 = 3^2 + 3.75^2 - 2 \times 3 \times 3.75 \cos \angle ABC\]

This gave me $\cos \angle ABC = 0.08611$ and then I can use the inverse cosine function, $\cos^{-1}$ to determine the measure of the angle $ABC.$ The $\cos^{-1}$ button on my calculator gave me the measure of the angle $CBE$ as 85.06 degrees so the measure of the angle $ABC$ is $180 - 85.06 = 94.94$ degrees.

The angle $DBC$ is a little more than one quarter of the way around the circle, in fact it is $\large \frac{94.94}{360}$ of the way around the circle. The area of the sector $BCD$ is this same fraction of the area of the circle so the area of the sector $BCD$ is $\large \frac{94.94}{360} \times \pi \times 3^2 = 7.46$ square inches.

The area of the triangle $BEC$ is one half the base times the height and I am going to use $|BE|$ as the base and $|EC|$ as the height. You know that $|BC| = 3$ inches and the measure of the angle $CBE$ is 85.06 degrees. $\large \frac{|EC|}{|CB|} = \sin \angle \normalsize CBE$ and $\large \frac{|BE|}{|CB|} = \cos \angle \normalsize CBE.$ Thus the area of the triangle $BEC$ is given by

\[\frac12 \times 3^2 \times \sin \angle CBE \times \cos \angle CBE = 0.39 \mbox{ square inches}\]

Hence the area of the orange region above the line segment $DE$ is $7.64 + 0.39 = 8.03$ square inches.

Penny