| |||
| Math Central | Quandaries & Queries |
|
Question from Nicole, a student: What is a common chord between two circles and how is it found in the problem: Two circles intersect and have a common chord, the radii of the circles are 13 and 15, the distance between the circle's centers is 14, find the common chord. |
Hi Nicole,
I can show you one method that works. There may be others.
In my diagram the common chord, AC, intersects the line segment the joins the centers at E. Angle AED is a right angle. Can you see why? Hence angle BEA is also a right angle. Thus triangles AED and BEA are right triangles.
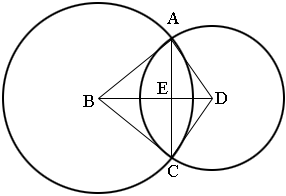
The length of EA is half the length of the common chord so I am going to call this length $h.$ Let the length of BE be $x$ then the length of ED is $14 - x.$ The length of AB is 15 and the length of DA is 13.
Use the fact that triangles ABE and EDA are right triangles and write down what Pythagoras Theorem says about there triangles. This gives you two equations in $x$ and $h$ which you can solve for $x$ and then determine $h.$
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.