A uniform probability density function

HOME

Math Central

Quandaries & Queries

Question from Noeline, a student:

Question:
The label on a bottle of liquid detergent shows contents to be 12 ounces per bottle. The production operation fills the bottle uniformly according to the following probability density function:
f(x) = 8 for 11.975 ≤ x ≤ 12.10
and
f(x) = 0 elsewhere

a. What is the probability that a bottle will be filled with 12.02 or more ounces?
b. What is the probability that a bottle will be filled between 12 and 12.05 ounces?
c. Quality control accepts production that is within .002 ounces of number of ounces shown on the container label. What is the probability that a bottle of this liquid detergent will fail to meet the quality control standard?

Hi Noeline,

Here is a graph of the probability density function.

density function

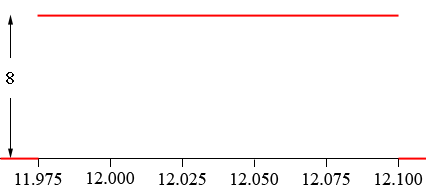
The probability that a bottle is filled with an amount between $a$ ounces and $b$ ounces is the area of the region bounded above by the density function, below by the X-axis and between $a$ and $b.$ for example the probability that a bottle will be filled with between 11.980 and 12.001 ounces is the area of the region coloured blue in the diagram below.

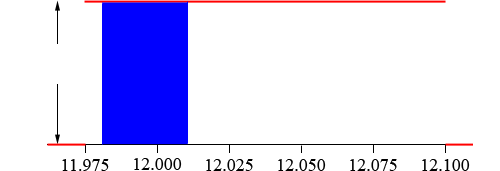
density function

This is a rectangle which is 8 units high and $12.010 - 11.980 = 0.030$ units wide. Hence its area is $8 \times 0.030 = 0.24$ square units. Thus the probability that a bottle will be filled between 11.980 and 12.010 ounces in $0.24.$

Now you try the problem you sent and write back if you need more help.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.