| |||
| Math Central | Quandaries & Queries |
|
Question from Noriz, a student: A cylinder is circumscribed about a right prism of altitude 12.6cm. Find the volume of the cylinder if the base of the prism is an isosceles triangle of sides 3cm by 3cm by 2cm. |
Hi Noriz,
I assume this is a circular cylinder which implies that its volume is the area of the circular base times the height. The area of a circle is $\pi r^2$ where $r$ is the radius so the challenge is to find $r.$
The circumcenter of a triangle is the point which is the center of a circle that includes the vertices of the triangle on its circumference. The circumcenter is the point where the right bisectors of two sides of the triangle meet. Can you se why?
To find the circumcenter and then the radius of the circumscribed circle I would put the triangle on the plane with its base on the X-axis and a vertex on the Y-axis as in the diagram.
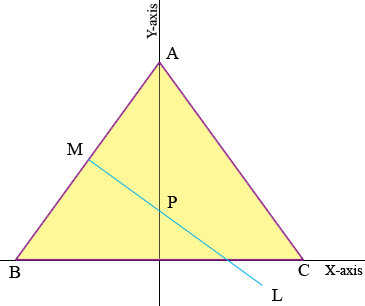
By the symmetry the circumcenter is on the Y-axis. M is the midpoint of AB and the line L is perpendicular to AB so the circumcenter is on L. Thus P is the circumcenter.
To fid P first find the coordinates of M and then the equation of the line L. Find where L intersects the Y-axis.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.