Hi Panny,

Many triangles have the same perimeter but different areas.

Suppose I start with everyone's favourite right triangle, the one with sides of length 3, 4 and 5 units.

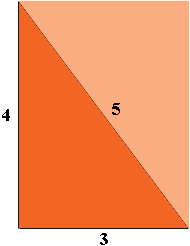
This triangle is half the rectangle with sides of length 3 and 4 units so its area is half the area of the rectangle. Hence its area is $\frac12 3 \times 4 = 6$ square units. Its perimeter is $3 + 4 + 5 = 12$ units.

Here is another triangle with a perimeter of 12 units. It is the isosceles triangle $ABC$ with base $AB$ of length 2 units and hence, since its perimeter is 12 units, the sides have length

\[\frac12 (12 - 2) = 5 \mbox{ units. }\]

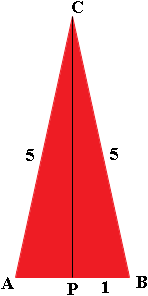
P is the midpoint of $AB$ and hence the height$|PC|$ of triangle $ABC$ can be found using Pythagoras' Theorem

\[|PC| = \sqrt{5^2 - 1^2} = \sqrt{24} = 4.8990 \mbox{ units.}\]

Thus the area of triangle $ABC$ is

\[\frac12 |AB| \times |PC| = 1 \times 4.8990 = 4.8990 \mbox{ square units.}\]

So this triangle has a perimeter of 12 units and yet its area is less than 5 square units.

That was fun! Let's do it again. This time make $|AB| = 0.2$ units. What are the lengths of the other two sides if the perimeter is to remain as 12 units? What is the area of the triangle?

What if $|AB| = 0.002$ units or $0.0002$ units or $0.0000002$ units?

Penny