Hi Patience,

Did you draw a diagram?

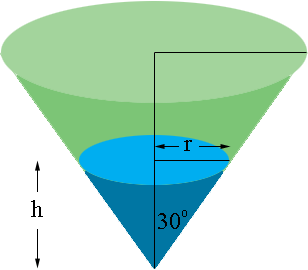
The volume of water in the tank is $V = \large \frac13 \pi \; r^2 h.$ $V$ and $h$ are both functions of time $t$ and the rate of change of the volume is $ \large \frac{dV}{dt}.$

From the diagram what trig function relates $h, r$ and the angle measure of 30 degrees? Use this to express $r$ as a function of $h.$ Substitute into the expression for the volume so that you have $V$ as a function of $h$ alone. Differentiate implicitly with respect to $t$ to obtain a relationship involving $\large \frac{dV}{dt}, \frac{dh}{dt}$ and $h.$ Substitute for $\large \frac{dV}{dt}$ and $h$ and solve for $\large \frac{dh}{dt}.$

Penny