A reservoir has the shape of an inverted cone

HOME

Math Central

Quandaries & Queries

Question from Roger, a student:

a reservoir has the shape of an inverted cone whose cross section is an equilateral triangle. if water is being pumped out of the reservoir at a rate of 2m^3/sec, at what rate is the depth of the water changing when the depth is 40 meters?

Roger,

My diagram shows the water in the reservoir when the height is $h$ meters. $ABC$ is an equilateral triangle and $D$ is the midpoint of $AB$ so that $r$ is the radius of the circular top of the water.

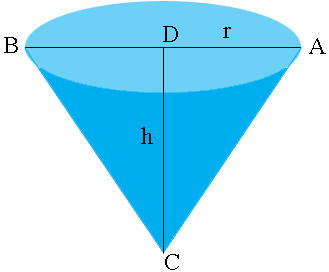
reservoir

What are the measure of the angles $CAD$ and $DCA?$ Write $r$ in terms of $h.$ The volume of water, $V$ is given by $\frac13 \pi r^2 h.$ Write $V$ as a function of $h$ and use the calculus you know to complete the problem.

Write back if you need more assistance.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.