Translation of a graph - Math Central

HOME

Math Central

Quandaries & Queries

Question from Sean, a student:

the information is thus:
$f(x)=3(x+1)^2-2$
I wish to translate up 2 units and move 2 units right.
Using basic translation I would guess that makes it $f(x)=3(x-1)^2$
but this strikes me as a quadratic formula, by means of the ^2
so wouldn't that start to make $y=f(x-2) +2$ where $y=[((3(x+1)^2)-2)-2]+2?$
if so then:
$y=([(3(x+1)^2)-2]-2)+2$
$y=([$
... I think I got lost, my problem is that I think I'm over-complicating things

My question is: Would my answer be s simple as f(x)=3(x-1)^2 or is it a more complicated answer which will get me lost?

Hi Sean,

You are asked to translate up 2 units and to the right 2 units. You can do this by moving the X-axis down 2 units and the Y-axis to the let 2 units. Below is the graph of the function $y = 3(x + 1)^2 - 2$ with the axes in black. The instructions are to move the axes to the red lines.

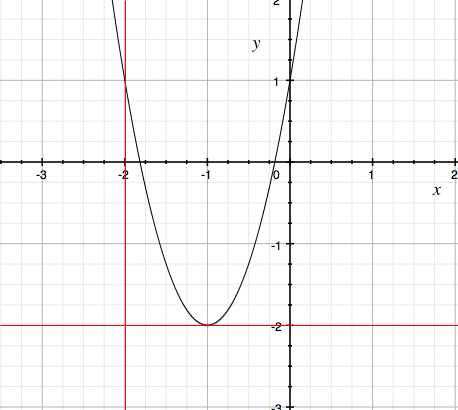
graph

The shape of the graph hasn't changed, all that has changed is that a point on the graph of $y = 3(x + 1)^2 - 2$ has its X-coordinate and Y-coordinate each increased by 2 relative to the new axes. The equation of the graph relative to the new coordinates is $y = 3(x - 1)^2$

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.