Hi,

The conventional way to define the trig functions is to start with an acute angle $\theta,$ that is an angle with measure $\theta$ between $0$ and $90$ degrees. You then draw a right triangle having one angle with measure $\theta$ degrees and label the three sides.

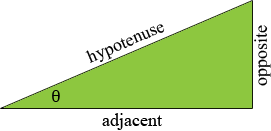
The longest side of the triangle is called the hypotenuse, the side opposite the angle $\theta$ is called the opposite side, the third side is called the adjacent side. The definitions of $\sin \theta$ and $\cos \theta$ are then given by

\[\sin \theta = \frac{\mbox{opposite}}{\mbox{hypotenuse}}\]

and

\[\cos \theta = \frac{\mbox{adjacent}}{\mbox{hypotenuse}}.\]

The tangent of $\theta$ is then defined in one of two ways,

\[\tan \theta = \frac{\mbox{opposite}}{\mbox{adjacent}}\]

or

\[\tan \theta = \frac{\sin \theta}{\cos \theta}.\]

You can check that the two definitions of the tangent are equivalent.

For angles that have measure larger than $90$ degrees or measure smaller than $0,$ that is with a negative measure, the definitions are more convoluted.

I want to show you definitions of the sine and cosine that are valid for any angle and then you can use my second definition for the tangent.

Start by drawing a unit circle, that is a circle with radius 1, and centre at the origin $O$. Draw a ray from the origin at an angle of measure $\theta$ degrees measured counterclockwise from the X-axis. Let $P$ be the point where the ray intersects the circle. In my diagram below I selected an angle with measure between $0$ and $90$ degrees. This will allow you to see that my definition agrees with the definition in terms of the triangle given above.

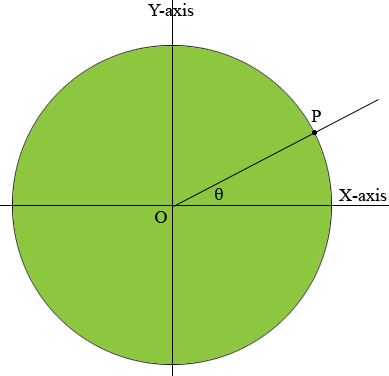
Define $\cos \theta$ as the X-coordinate of $P$ and $\sin \theta$ as the Y-coordinate of $P$ and $\tan \theta = \large \frac{\sin \theta}{\cos \theta}.$

Here is the diagram again with one extra line segment and with one extra point labeled.

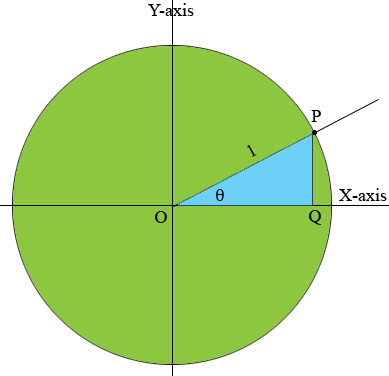
Looking at the triangle $POQ,$ the X-coordinate of $P$ is $|OQ|$ and hence using my definition

\[\cos \theta = |OQ| = \frac{|OQ|}{1} = \frac{\mbox{adjacent}}{\mbox{hypotenuse}}.\]

Likewise

\[\sin \theta = \frac{\mbox{opposite}}{\mbox{hypotenuse}}.\]

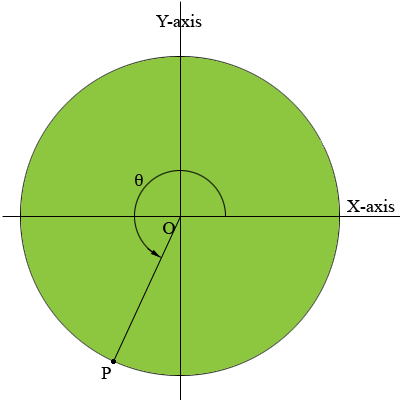
One big advantage of defining the the sine and cosine this way is that the definition is valid regardless of the size of the angle. For example in my diagram below the cosine and sine of the angle $\theta$ are the X and Y-coordinates of $P$ and it is clear from the diagram that they are both negative.

Harley