| |||
| Math Central | Quandaries & Queries |
|
Question from Tewodros, a student: Let f(x) = e^x and g(x) = x^1/2 both be defined on [0,1]. Consider the region bounded by f(x), g(x), x = 0, x = 1. Rotate this region about the y-axis and determine the volume using the shell method. |
Hi,
I'll start the problem for you.
The region to be rotated about the y-axis is shown in the diagram along with a dark strip at approximately $x$ on the x-axis, of thickness $\Delta x,$ and height $e^x - x^{1/2}.$
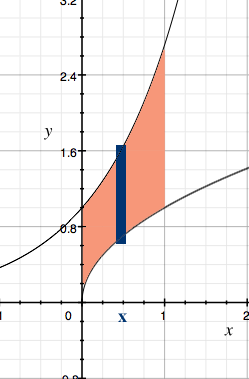
When this strip is rotated about the y-axis it produced a cylindrical shell of height $e^x - x^{1/2},$ thickness $\Delta x$ and radius $x.$ The volume of this shell is approximately its circumference times its height times its thickness, that is
\[2 \pi x \times (e^x - x^{1/2}) \times \Delta x.\]
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.