Hi Tim,

I drew your cup (not to scale) and then extended it downwards to form a cone. The dimensions are in inches.

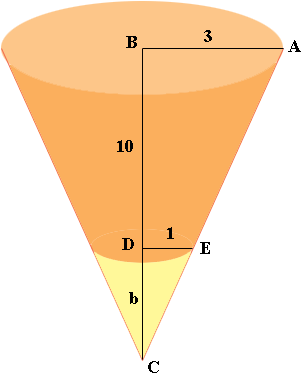
Triangles $ABC$ and $EDC$ are similar and hence

\[\frac{3}{10 + b} = \frac{1}{b}.\]

Solving for $b$ gives $b = 5$ inches.

Now suppose that the water has been flowing into the cup for a while and the height of the water is $h(t)$ inches and the radius of the top of the water is $r(t)$ inches. $t$ is time in minutes.

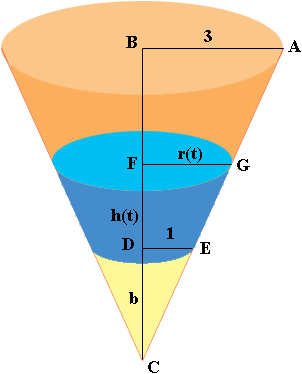
The volume of a cone of radius $r$ inches and height $h$ inches is $\frac13 \pi r^2 h$ cubic inches and hence, since $b = 5$ the volume of water in your cup $t$ minutes after the water begins to pour in is

\[V(t) = \frac13 \pi \; r(t)^2 (h(t) + 5) - \frac13 \pi \;1^2 5.\]

Can you complete the problem from here? Write back if you need more assistance.

Penny