| |||
| Math Central | Quandaries & Queries |
|
Question from Victoria, a student: Suppose you have a water tank in the shape of a truncated cone. The larger diameter is K, the smaller diameter is K/2, and the height is also K (all measured in meters). The force of gravity on an object of mass, m, is F=9.8m (measured in Newtons). The density of the water is 1000 kilograms per cubic meter. What is the volume of the tank and how much mass will the tank have when it is full? |
Hi Victoria,
I drew a diagram and extended the truncated cone to form a complete cone. I am assuming that K is measured in meters.
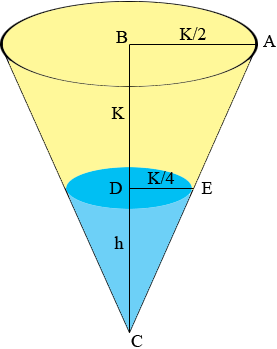
The volume of the tank is the volume of the large cone minus the volume of the small cone which I coloured blue. The height of the small cone is h meters. The volume of a cone is
\[\frac13 \pi \; r^2 t\]
where $r$ is the radius and $t$ is the height. Hence you can determine the volume of the tank if you can first determine the height $h$ of the small cone.
The key here is that the triangles ABC and EDC are similar. Thus
\[\frac{K + h}{K/2} = \frac{h}{K/4}\]
Solve for $h$ and then use this to calculate the volume of the tank in cubic meters. Every cubic meter of water in the tank weighs 1,000 kilograms so you can calculate the mass of the water in the tank.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.