Here is the diagram Wayne sent.

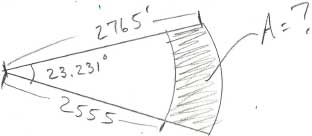
Hi Wayne,

Your diagram shows sectors of two circles, one of radius 2765 feet and the other of radius 2555 feet. The sectors have the same central angle that measures 23.231 degrees. The shaded region has an area which is the difference between the areas of the two sectors.

The area of a circle of radius $r$ units is $\pi r^2$ square units. A sector of a circle is a fraction of the circle and the size of the central angle tells you the fraction of the circle's area that is in the segment. There are $360$ degrees around the entire circle and if the central angle of a sector has measure $t$ degrees then the area of the sector is

\[\frac{t}{360} \times \pi \times r^2 \mbox{ square units.}\]

Hence the larger of the two sectors has area

\[\frac{23.231}{360}\times \pi \times 2765^2 \mbox{ square units.}\]

What is the area of the smaller sector? What is the area of the shaded region in your diagram?

Penny