Even if you want your 5-pointed star to be REGULAR, there will be two possible answers to your problem. Let's start with what we mean by a REGULAR PENTAGRAM, then look at the possible ways to compute its area.

Begin with a point A on a circle of radius r. (You can set r = 12.517 at the end. For now, any fixed number r will do.) Define the second vertex to be the point B on the circle so that the angle BO makes with AO is $2 \times \large \frac{360}{5} = 144$ degrees. Similarly, angle COB = DOC = EOD = AOE =144 degrees. This 5-pointed star is regular because every side (such as AB) has the same length and the angles between adjacent sides (such as AB and BC) are equal (to 36 degrees).

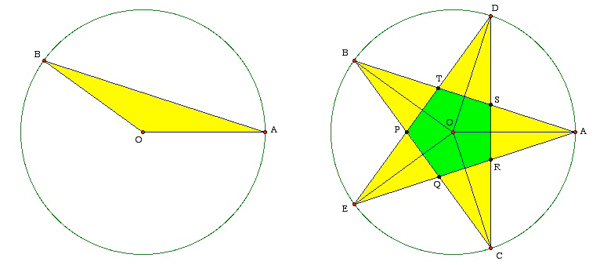
The way many mathematicians think of the area is to take a basic component -- here the triangle BOA -- and use it to tile the object whose area we wish to compute. We then simply compute the area of the initial triangle and multiply by 5 to get the area of the pentagram: The height of the triangle is $r \times \cos 72$ while its base is $2 \times r \times \sin 72.$ The area of the generating triangle is therefore

\[\mbox{AREA(BOA}) = \frac12 \times \mbox{base} \times \mbox{height} = r^2\times \sin 72 \times \cos 72.\]

Our first answer to your problem is therefore $5 \times r^2 \times \sin 72 \times \cos 72.$

You will have noticed that using this rotation method for obtaining the area means that the central pentagon region (labeled PQRST and colored green in the figure) has been counted twice. It makes sense to compute the area this way because that's the way our pentagram was generated. It is also possible to produce the star figure by starting with the regular green pentagon and sticking a yellow triangular "hat" (such as SRA) on each of its five edges. But there remains the question of the shape that triangular hat. It can be tall and thin (with an area as large as we wish to make it), or it can be short and fat (with an area close to zero). To make the star regular, we DEFINE its sides to be extensions of the sides of the starting pentagon. Now we can easily determine the area of the star figure (which we now agree to consist of a pentagon and five triangles) by subtracting the area of the green pentagon from the area of the pentagram we computed above. The pentagon is composed of five congruent isosceles triangles such as OPQ. The height of this triangle we know to be $r \times \cos 72;$ its base therefore is $2 \times r \times \cos 72 \times \tan 36.$ The area is

\[ \mbox{AREA(OPQ)} = r^2 \times (\cos 72)^2 \times \tan 36.\]

The area of the star figure is therefore obtained by subtracting $5 \times r^2 \times (\cos 72)^2 \times \tan 36$ from $5 \times r^2 \times \sin 72 \times \cos 72.$

Chris