A max/min problem - Math Central

HOME

Math Central

Quandaries & Queries

Question from bailey, a student:

Hi there,

A right angled triangle OPQ is drawn as shown where O is at (0,0).
P is a point on the parabola y = ax – x^2
and Q is on the x-axis.

Show that the maximum possible area for the triangle OPQ is (2a^3)/(27)

It has been bugging me from the test.
Thanks :)

Hi Bailey

I expect the diagram looks something like this. I gave $Q$ the coordinates $(x,0).$

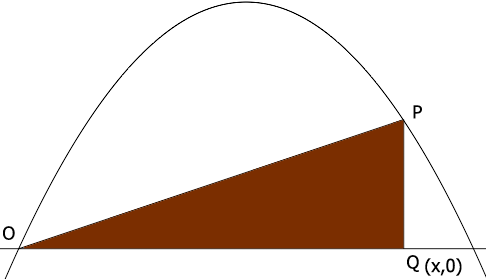
parabola and triangle

What is the y-coordinate of $P?$ That's the height of the triangle. What is the area of this triangle? Use the calculus you know to find the value of $x$ that maximizes the area. What is the area at for value of $x?$

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.