Hi Bianca,

Let's think about this geometrically for the moment. $y = x^2 - 2x$ is a parabola and $y = k x - 4$ is a line so you have three possible cases.

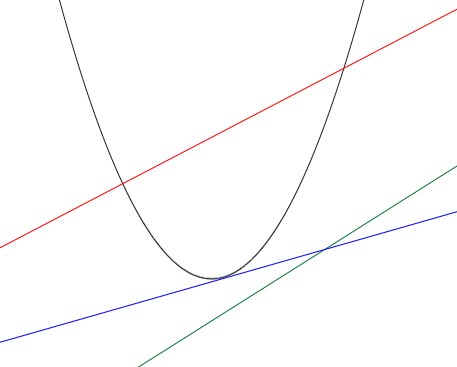
1. The line could not intersect the parabola at all (the green line in the diagram),
   
   
2. the line could intersect the parabola at two points (the red line in the diagram) or,
   
   
3. the line could intersect the parabola at exactly one point (the blue line in the diagram).

Now think algebraically.

To determine where the parabola $y = x^2 - 2 x$ and the line $y = k x - 4$ intersect substitute $y$ from the line equation into the equation of the parabola to obtain

\[k x - 4 = x^2 - 2 x.\]

Simplify and set up the general quadratic expression to solve for $x,$

\[x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}.\]

For your problem the important part of this expression is the discriminant,

\[D = b^2 - 4 a c.\]

If $D$ is negative Then the square root is imaginary and there is no solution (case 1). If $D$ is $0$ then there is exactly one solution (case 3) and if $D$ is positive there are two solution (case 2).

Penny