Hi Bryan,

The key to solving this is Pythagoras Theorem. It amazes me how often the key to solving a practical problem is Pythagoras Theorem.

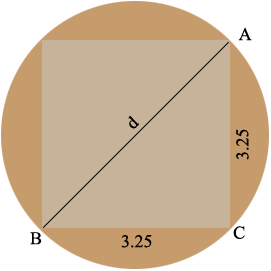
Suppose the diameter of the round stock is $d$ inches. In the diagram above the triangle $ABC$ is a right triangle and Pythagoras Theorem states that for a right triangle the square of the length of the hypotenuse (the long side) is the sum of the squares of the lengths of the other two sides. Thus

\[d^2 = 3.25^2 + 3.25^ 2 = 10.5625 + 10.5625 = 21.125 \mbox{ square inches}\]

and thus

\[d = \sqrt{21.125} = 4.596 \mbox{ inches}\]

I hope this helps,
Harley