A gravel pile in the shape of a triangular pyramid

Math Central

Quandaries & Queries

Hello,

Right now I am stuck and I feel embarrassed because I feel like the answer is so easy I should know it.

I am working on a project and need to find a volume of gravel it will take to occupy this triangular prism like area. I am not sure what formulas I should use whether it be that for the volume of a pyramid or something more complex? Basically it forms a right triangle at one side then from there all points slope to one singular point about 10412mm away.
I am attaching a picture drawn up in paint with the actual dimensions to clear up any confusion.

Thank you for any help.
Casey

Hi Casey,

Here is the diagram you sent. I labeled one vertex $P$ and shaded one face. You also gave us that $A = 10412.98 \mbox{mm, } B = 1955.8 \mbox{ mm, and } C = 227 \mbox{ mm.}$

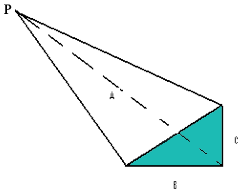
triangular pyramid

This shape is called a triangular pyramid and the volume of a triangular pyramid is

\[\frac13 \times \mbox{ the area of the base } \times \mbox{ the height.}\]

In your situation I would take the face I shaded green as the base since its area is easy to calculate. The area of the base is

\[\frac12 B \times C.\]

The height is the perpendicular distance from the base to the vertex $P.$ I can't tell from your diagram if $A$ is the height, but if it is not you will need a way to find the height.

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.