Hi Charles,

I agree with your calculation. The wedge to be removed sits on an arc of length 286.479 (inches?). You didn't include units.When you roll up the wedge to form a cone

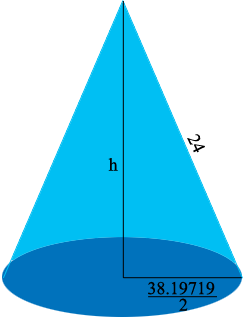
the slant height of the cone is the radius of the "round" and the radius of the circular base is half its diameter. I let the height be $h$ inches and then the triangle in the diagram is a right triangle so Pythagoras Theorem gives you

\[h^2 + \left( \frac{38.19719}{2} \right)^2 = 24^2 .\]

Thus

\[h = \sqrt{24^2 - \left( \frac{38.19719}{2} \right)^2} = 14.534 \mbox{ inches.}\]

Harley