Hi David,

I would use a graphical method to tell me how many solutions there are and their approximate values before attempting to find the solutions. There are two ways I can see to do this.

Method 1.

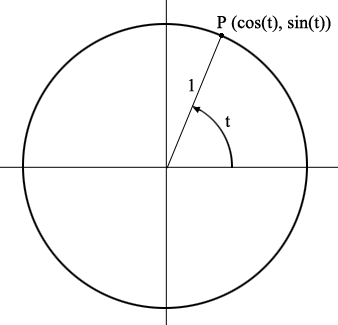
A point $P$ on the unit circle with centre at the origin has coordinates $(\cos(t), \sin(t))$ where $t$ is the angle, measured counterclockwise from the x-axis to the ray joining the origin to $P.$

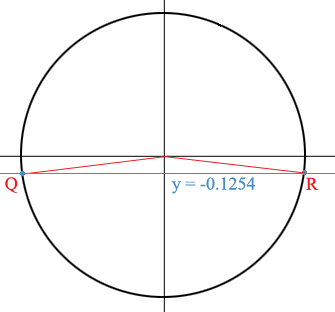
You are looking for $t = 3x$ where $\sin(t) = -0.1254$ and $\sin(t)$is the second coordinate of $P$ so I added the line $y = -0.1254$ to the graph.

The line intersects the circle at two points, $Q$ and $R$ where the angle $t = 2x$ measured counterclockwise from the x-axis to the ray from the origin to $Q$ is slightly more than $180^o$ and the angle $t = 2x$ measured counterclockwise from the x-axis to the ray from the origin to $R$ is slightly less than $360^o$.

Method 2.

Look at the graph of $y = sin(t)$.

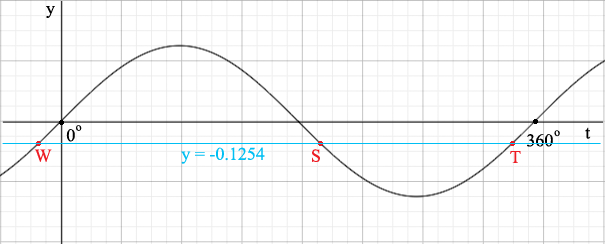
Add the line $y = -0.1254$ to the graph.

Again we see two solutions $S$ and $T,$ one where $t = 3x$ is slightly more than $180^o$ and the other where $t = 3x$ is slightly less than $360^o$.

Whichever graph you choose to look at you now know there are two solutions to $\sin 3x = -0.1254 \mbox{ with } 0<x<360^o$ and you know the approximate values of $t = 3x$. Now it's time to use your calculator.

When I set my calculator to degrees rather than radians and asked for $\sin^{-1}(-0.1254)$ I got a response of $-7.204^o$.

In my first method that's the point $R$ where the angle is measured in a negative direction, clockwise, so measured counterclockwise that's $t = 3x = 360^0 - 7.204^o$. What's the angle measure of the point $Q?$

In my second method the calculator returned the point $W$ which is $7.204$ units to the left of the origin so $T$ is $7.204$ degrees less than $360.$ What is the $t$ coordinate of $S?$

I am sorry this is so long winded but I don't know which graphical method you prefer.

Harley