Hi Dee,

I have names your players 1, 2, 3, 4 and 5 and placed them at the vertices of a regular pentagon. A line joining two vertices of the pentagon represents an instance when the two players at these vertices form a team.

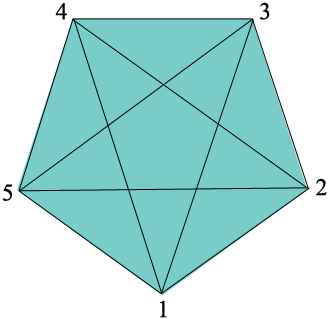
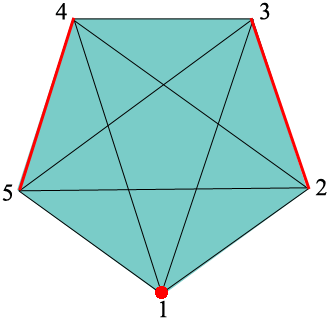
For the first round of play have person 1 sit out, 2 and 3 form a team and 4 and 5 form a team.

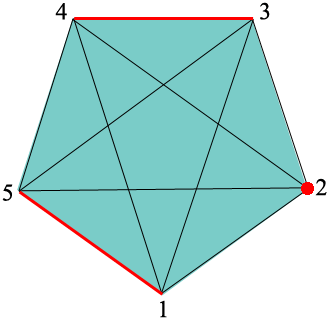
For the next round of play rotate the pentagon one fifth of a revolution counterclockwise, leaving the players unmoved. For this round player 2 sits out and players 3 and 4 form a team and players 5 and 1 form teams.

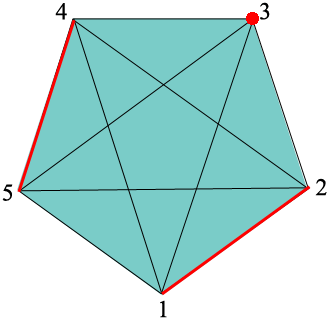
For the third round of play rotate the pentagon again one fifth of a revolution counterclockwise, leaving the players unmoved. For this round player 3 sits out and players 2 and 5 form a team and players 1 and 2 form teams.

Repeat this process until it is time for player 1 to sit out again. This time, round 6, have players 3 and 4 and players 5 and 2 form teams.

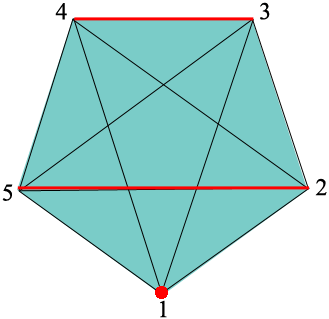
Rotate again to have player 2 sit out and players 4 and 5 and players 1 and 3 form teams. Continue rotating until player 1 is to sit out again. This will be round 11 and in this case have player 1 sit out and players 2 and 4 and players 5 and 3 form teams.

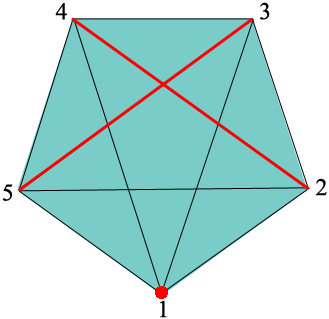
Continue to rotate the pentagon until you have completed 15 rounds of play. In these 15 rounds each player has sat out 3 times and each pair of players has formed a team 3 times.

Penny