Hi Don,

Id this how the top of the tank looks? If so I need to know where to place the smaller circle. Do you know where the center of the small circle is, or perhaps the distance between the centers of the circles?

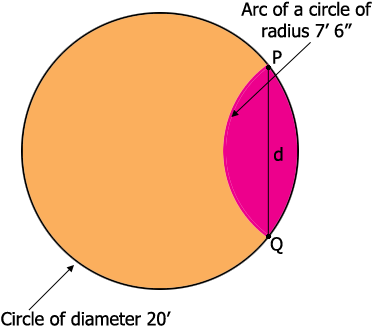
Harley

Don replied.

That is how the tank looks. I really don't know any other dimensions. How would I figure the volume in the smaller section?

I labeled two points $P$ and $Q$ in the diagram. Can you measure the distance $d$ from $P$ to $Q?$

Harley

Don replied.

I was able to measure the distance d. It is 8' 2"

Perfect!

I redrew the diagram and decided to use inches for the units of length.

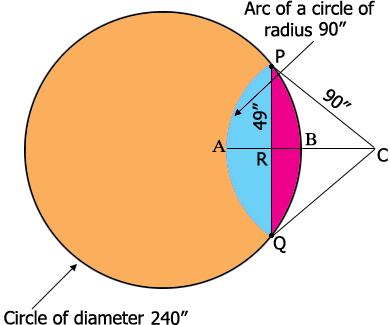
$C$ is the center of the smaller circle and $R$ is the midpoint of $PQ.$

The volume of the smaller compartment of your tank is the total area of the red and blue regions of the diagram, times the height of the tank which is 236". I'm going to start by finding the area of the blue region. To do this I will find the area of the sector $CPAQ$ and then subtract the area of the triangle $CPQ.$

The triangle $PRC$ is a right triangle so from Pythagoras' Theorem

\[|RC| = \sqrt{90^2 - 49^2} = 75.49 \mbox{ inches}\]

Hence the area of the triangle $PQC$ is $\large \frac12 \normalsize \times |PQ| \times |RC| = 3699.01$ square inches.

The area of the sector $CPAQ$ is $\large \frac12 \normalsize \times r^2 \times \theta$ square inches where $r$ is the radius in inches (90 inches) and $\theta$ is the measure of the angle $QCP$ in radians. The angle $QCP$ is twice the angle $RCP$ and the measure of the angle $RCP$ is $\sin^{-1} \large \frac{49}{90} \normalsize = 0.5757$ radians (32.99 degrees). Hence the measure of the angle $QCP$ is $2 \times 0.5757 = 1.1515$ radians and the area of the sector $CPAQ$ is

\[\frac12 \times 90^2 \times 1.1515 = 4663.39 \mbox{ square inches.}\]

Finally the area of the region shaded blue in the diagram is $4663.39 - 3699.01 = 964.4$ square inches.

In a similar fashion you can find the area of the region shaded red in the diagram. I got $689.6$ square inches.

Hence the total area of the red and blue regions is $964.4 + 689.6 = 1654$ square inches and the volume of the smaller section of your tank is $1654 \times 236 = 390,344$ cubic inches.

If you want to express the volume in other dimensions then Google will do it for you. For example if you want the volume in gallons then type 390344 cubic inches in gallons in the Google search window.

Harley