| |||
| Math Central | Quandaries & Queries |
|
Question from Elizabeth, a student: 1) The figure below shows a bridge across a river. The arch of the bridge is a parabola and the six vertical cables that help support the road are equally spaced at 4-m intervals. Figure B shows the parabolic arch in an x-y coordinate system, with the left-end of the arch at the origin. As indicated in Figure B, the length of the leftmost cable is 3.072 m. I/m suppose to find the (x-h)^2=-4a(y-k) equation for this word problem and I really do not know where to begin. Afterwards, I need to find the lengths of the other cables and the maximum height of the arch of the road as well which I am very confused about |
Hi Elizabeth,
This is the diagram I drew from your description.
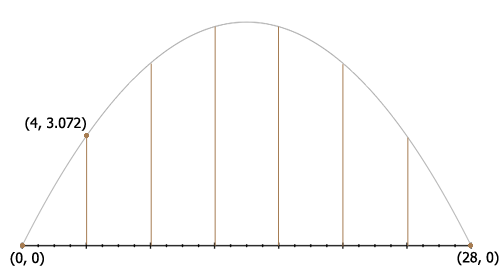
The parabola passes through $(0, 0)$ and there are 6 cables, 4 meters apart so the bridge is $4 \times 7 = 28$ metres long and hence the parabola passes through $(28, 0).$ The first cable is $3.072$ metres long and hence the parabola passes through $(4, 3.072).$
Substitute $(0, 0)$ and $(28, 0)$ into the equation of the parabolas, $(x-h)^2=-4a(y-k)$ and you can then solve the resulting equations for $h.$ Do you see how to proceed from here?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.