Hi,

I assumed you wanted $\log$ to be the natural logarithm. If you want a different logarithm then the numbers will change but the process is the same.

First I graphed $y = 8 \times \log(x)$ and $y = x.$

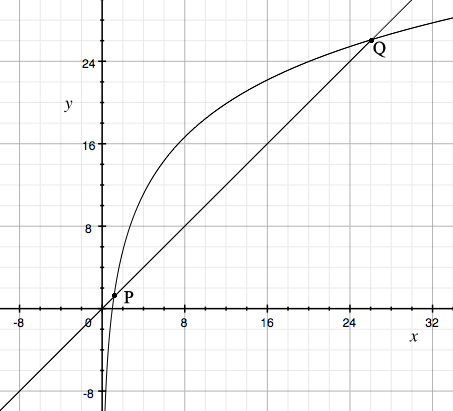
If $P$ and $Q,$ the points of intersection have coordinates $(x_1, x_1)$ and $(x_2, x_2)$ then the solution to $8 \log(x) >x$ is the interval $x_1 < x < x_2$.

The challenge is then to solve $8 \log(x) = x$ to determine $P$ and $Q.$ Unfortunately that is not straightforward. I used Wolfram Alpha, and typed in solve 8 * log(x) = x. Try it.

Harley