| |||
| Math Central | Quandaries & Queries |
|
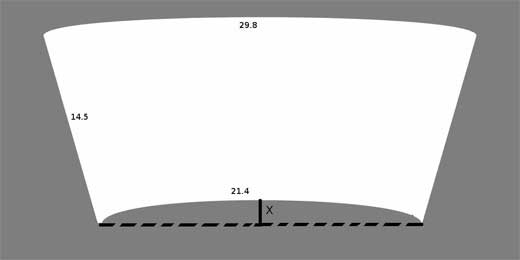
I'm trying to make a label to cover the entire outer area or a plastic cup. I know there must be a way to figure out the dimensions needed, but I can't seem to figure it out. The circumference of the bottom of the cup is 21.4cm and the circumference at the top of the cup is 29.8cm. The cup is 14.5cm tall. What should the height of the arc from the plane connecting the two ends of the 21.4cm arc. I attached a diagram where x is the value I'm looking for. I'm guessing there is some simple relationship between the length of a line and the arc needed to turn that line into a perfect circle, but I don't know what it is. Can you figure this out and share it with me? Thanks. |
This is the diagram Kevin sent
Hi Kevin,
I redrew your diagram because I want to add to it.
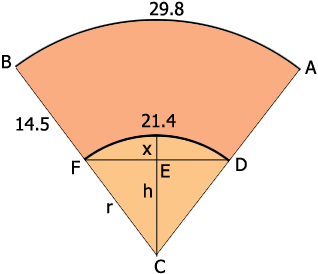
The sectors $ABC$ and $DFC$ are similar and hence 29.8 is to 21.4 as $|BC|$ is to $|FC|,$ that is
\[\frac{29.8}{21.4}= \frac{r + 14.5}{r}\]
Solve for $r.$
If $a$ is the length of an arc of a circle or radius $r$ and the arc is subtended by the angle with measure $\theta$ radians than $a = r \times \theta.$ Hence using the arc $DF$ which is subtended by the angle $FCD$ we get
\[21.4 = r \times \theta,\]
where $\theta$ is the measure of the angle $FCD$ in radians.
You know $r$ and hence you can solve for $\theta.$
The angle $CF$ is a right angle and and the measure of the angle $FCE$ is $\large \frac{\theta}{2}.$ Hence
\[\cos \frac{\theta}{2} = \frac{h}{r}.\]
This allows you to solve for $h$ and $x = r - h.$
(When using your calculator to calculate $\cos \frac{\theta}{2}$ make sure you have it set on radians and not degrees.)
Write back if you need more assistance,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.