Hi Ky,

If you draw a reasonably careful diagram of a triangle with side lengths 3, 4 and 5 inches you will see that the angle between the sides of length 3 and 4 inches appears to be a right angle. Pythagoras' Theorem tell us that if a right triangle has side lengths a, b and c units with the right angle between the sides of length a and b units then $a^2 + b^2 = c^2$. The converse of Pythagoras' Theorem is also true, that is if a triangle has side lengths a, b and c units and $a^2 + b^2 = c^2$ then the angle between the sides of length a and b units is a right angle. Since $3^2 + 4^2 = 5^2$ your triangle has a right angle between the sides of length 3 and 4 units. This is important because it allows you to use the trig functions sine, cosine and tangent with this triangle.

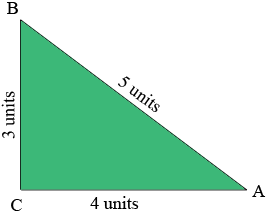
Now you are ready to find the angle measurements. For example in my diagram the sine of the angle measurement at A is $\large \frac{3}{5},$ and hence the angle measurement at A is given by $\sin^{-1}\left(\large \frac35\right).$ Use your calculator to find this value but make sure that your calculator is in the degree mode rather than the radian mode. Use the other two inverse trig functions at the angle A to determine that they all give the same value as the angle measurement. Repeat at B.

I hope this helps,
Penny