Hi,

I want to use the cartesian graph of $y = \cos(x)$ for reference.

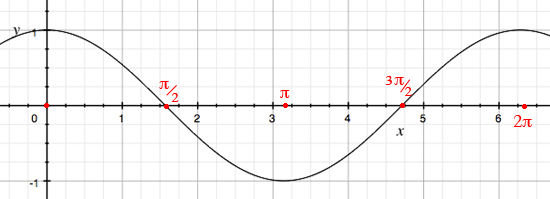
Now let's plot $r = 10 \cos(\theta)$ in polar coordinates for $0 \le \theta \le 2 \pi.$

$\cos(0) = 1$ and hence the graph starts at $(r, \theta_1) = (10,0)$ which is the point $P_1$ in my diagram.

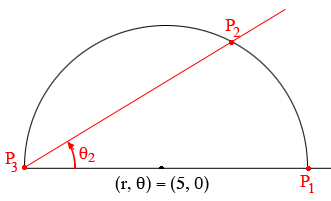
Now let $0 < \theta_2 < \frac{\pi}{2}$ then $\cos(\theta_2)$ is positive and resulting point $P_2$ is on the upper half of the circle with center $(5, 0)$ and radius 10 as in my diagram. When $\theta_3 = \frac{\pi}{2}$ then $\cos(\theta_3) = 0$ and the resulting point on the graph is $P_3$.

For $\frac{\pi}{2} < \theta le \pi$ as $\theta_4$ in my diagram, $\cos(\theta) < 0$ and the resulting point (for example $P_4$) is on the bottom half of the circle with center $(5, 0)$. When $\theta = \pi$ then $\cos(\theta) = -1$ and we are back at $P_1$.

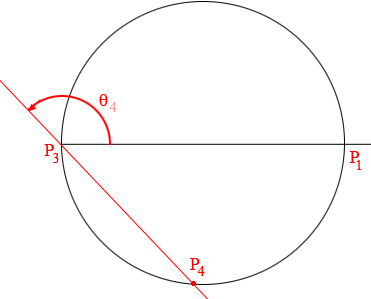
For $\pi < \theta \le \frac{3 \pi}{2}$ as $\theta_5$ in my diagram, $\cos(\theta)$ is still negative and the resulting point (for example $P_5$) is on the top half of the circle with center $(5, 0)$. When $\theta = \frac{3 \pi}{2}$ then $\cos(\theta) = 0$ and we are back at $P_3$.

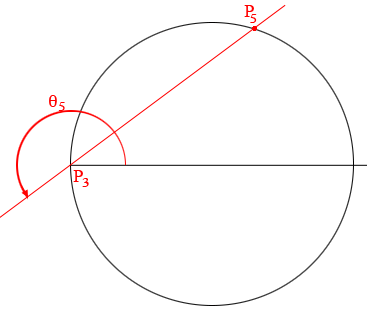
Finally for $\frac{3 \pi}{2} < \theta \le 2 \pi, \cos(\theta)$ is positive and the resulting point, as $P_5$ in my diagram is on the bottom half of the circle and when $\theta = 2 \pi$ we are back at $P_1$.

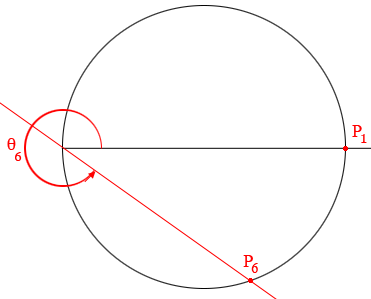
Hence as $\theta$ moves from $0$ to $2 \pi$ the point defined by $r = 10 \cos(\theta)$ moves twice around the circle with center $(r \theta) = (5, 0)$ and radius 10.

Penny

r.m replied

sir,
in reply to your answer for r=10cost in cylinderical coordinates. if we follow the same method as you explained to sketch r=sin(t/2),i expected graph to be in only first two quadrants, but the graph was covering all four quadrants ?
please help..

If $0 < \theta <2 \pi $ then $0< \large \frac{\theta}{2} \normalsize < \pi$ and $\sin \left(\large \frac{\theta}{2}\right) >0.$ Thus, for example if $\theta = \large \frac{3 \pi}{2}$ then

\[r = \sin \left(\frac{\theta}{2}\right) = \sin \left(\frac{3 \pi}{4}\right) = \frac{1}{\sqrt 2} = 0.70711\]

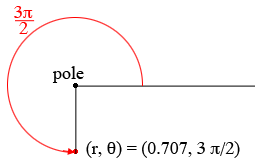
Penny