Hi Renu,

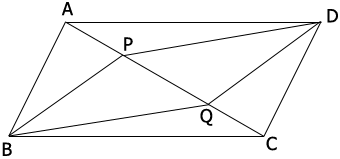
Since $BP$ and $DQ$ are parallel the measures of the angles $APB$ and $DQC$ are equal. Since $AB$ and $CD$ are parallel angles $PAB$ and $QCD$ are equal. Thus triangles $ABP$ and $CDQ$ are similar. But $|AB| = |CD|$ and hence triangles $ABP$ and $CDQ$ are congruent. Thus $|AP| = |CQ|.$

From this you can show that triangles $APD$ and $CQB$ are congruent. Do you see how? Hence the angles $APD$ and $CQB$ are equal and thus $PD$ and $QB$ are parallel.

Harley