Hi Sidra,

I think This is for a calculus class so you are expected to use integration. Here is my diagram.

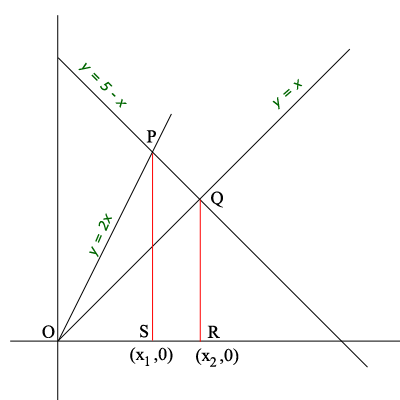
Solve the equation $y = 5 - x$ with both of the equations $y = x$ and $y = 2x$ to determine the coordinates $(x_1, y_1)$ and $(x_2, y_2)$ of $P$ and $Q$ respectively. The area of the triangle $POQ$ is the area of the triangle $POS$ plus the area of the trapezoid $PSRQ$ minus the area of the triangle $QOR.$ Each of these can be found using integration.

If I were to find this area for anything but a calculus class I certainly wouldn't use integration. First of all the line $y = x$ has slope 1 and the line $y = 5 - x$ has slope -1 and thus these line are perpendicular. Thus the triangle $POQ$ is a right triangle and thus if you find the lengths of $OQ$ and $QP$ you can calculate that area of the triangle using half the base times the height.

Even easier is to surround the triangle $POQ$ with the rectangle $TWOR.$

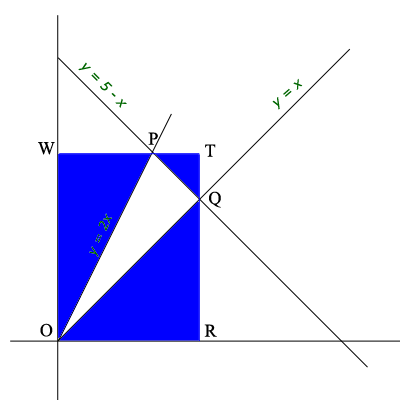
The area of the triangle $POQ$ is the area of the rectangle minus the sum of the areas of the three blue triangles. Each of these triangles is a right triangle with sides parallel to the coordinate axes and its area is easy to calculate.

Penny