| |||
| Math Central | Quandaries & Queries |
|
Question from Steven, a student: At a certain instant an aircraft flying due east at 240 miles per hour passes directly over a car traveling due southeast at 60 miles per hour on a straight, level road. If the aircraft is flying at an altitude of .5mile, how fast is the distance between the aircraft and the car increasing 36 seconds after the aircraft passes directly over the car? |
Hi Steven,
I drew a diagram of the situation $t$ hours after the plane was directly over the car. $P$ is the position of the plane, $C$ is the position of the car, $G$ is the point on the ground directly below the plane and $O$ is the point on the ground where the car was when the plane was overhead. The measure of the angle $GOC$ is $\large \frac{\pi}{4}$ radians. All the distances are in miles.
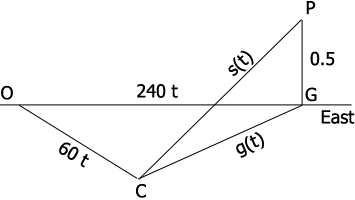
You are to find $s^{\prime}(t)$ when $t = 36$ seconds. Since triangle $PCG$ is a right triangle, if you can find $g(t)$ you can use Pythagoras theorem to obtain an expression for $s(t)$ which you can then differentiate and evaluate at $t = 36$ seconds. Make sure you convert $36$ seconds to hours first.
How do you determine $g(t)?$ I would use the Law of Cosines.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.