Hi Tehmas,

In this problem it's not the intercepts that are important, it's the x-coordinates of the places where the graphs cross. Let me illustrate with a simpler question.

Solve $x^2 - 2 > x$ using a graphical approach

I first solve $x^2 - 2 = x$ to determine where the graphs cross. Simplifying and solving I found that the graphs cross at $x = -1$ and $x = 2.$ I now sketch a graph. In my case $f(x) = x^2 - 2$ (a parabola) and $g(x) = x$ (a line) are simple enough that I can graph them easily.

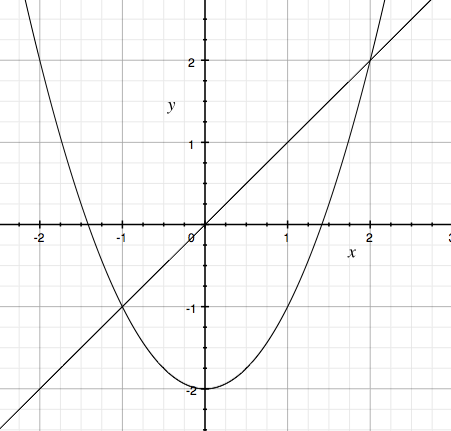
Asking where $x^2 - 2 > x$ is asking for the region or regions where the parabola lies above the line. It is clear from the graph that there are two such regions $\{x\; |\; x < -1\}$ and $\{x \;|\; x > 2\}.$

Penny

Tehmas wrote back

I understand the example u gave me but couldn't apply it to the original question

If you understand the example then I think the most difficult and labourious part of the solution is finding where the graphs intersect, that is solving

\[2x^4+x^3-37x = 26x^2+12\]

or

\[2x^4+x^3 - 26 x^2 -37x -12 = 0.\]

This problem is designed so that some of the intersection points have integer x-coordinates so that you can use the Factor Theorem to factor the quartic polynomial. Once you have the intersection points solving the inequality is straightforward.

Suppose that $x = a$ and $x = b$ are the x-coordinates of two consecutive points where the graphs intersect. Choose some number $c$ between $a$ and $b$ and evaluate $f(x) = 2x^4+x^3-37x$ and $g(x) = 26x^2+12$ at $x = c.$ If $f(c) > g(c)$ then $f(x) > g(x)$ for the entire interval $a < x < b$ since the graphs don't meet again until $x = b.$ Likewise if $g(c) > f(c)$ then $g(x) > f(x)$ for all x satisfying $a < x < b.$

This is a example where I would use some software either to help with the calculations or to check my work. I used Wolfram Alpha and typed

Solve 2x^4+x^3-37x = 26x^2+12

into the input field.

Penny