Hi Tim,

You know that the radius of the circle is

\[\frac{1500^2 + 300^2}{300 + 300} = 3900 \mbox{ mm}\]

and hence the circumference of the circle is

\[2 \times \pi \times 3900 \mbox{ mm.}\]

You want the length of the arc from $A$ to $B$ in my diagram below.

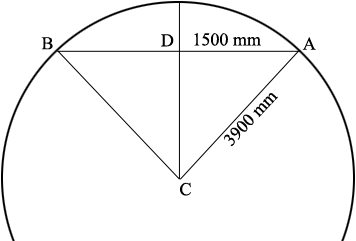
To determine this I need the measure of the angle $BCA$ which I am going to call $t$ degrees. The angle $ADC$ is a right angle and the measure of the angle $DCA$ is $\frac{t}{2}$ and thus

\[\sin(\frac{t}{2}) = \frac{1500}{3900}.\]

I used the $\sin^{-1}$ button on my calculator, making sure it was set on degrees and found that $\frac{t}{2} = 22.6199$ degrees. Thus $t = 2 \times 22.6199 = 45.239$ degrees.

This is very close to 45 degrees which would be $\frac14$ of the way around the circle and would give the length of the arc from $A$ to $B$ as $\frac14$ of the circumference of the circle. Thus the length of the arc is approximately

\[\frac14 \times 2 \times \pi \times 3900 \mbox{ mm.}\]

But the fraction is not $\frac{45}{360} = \frac14$ it's $\frac{45.239}{360}$ and thus the length of the arc is

\[\frac{45.239}{360} \times 2 \times \pi \times 3900 \mbox{ mm.}\]

Penny