| |||
| Math Central | Quandaries & Queries |
|
Question from Tizoc, a student: I am in a trig class and I have a conflict. When solving the length of a side, I know what trig function to use, but I do not know what angle to use in a calculator. To make this a little more understandable, if I have all the angles available in a right triangle and I use the tangent function, how do I know what to use? |
Hi Tizoc,
I'm not sure I understand your question but I'll give it a try. I expect that your textbook or teacher have told you that
\[\tan(A) = \frac{\mbox{opposite}}{\mbox{adjacent}}.\]
In my diagram of a right triangle, since I am interested in the angle at $A$ the side opposite to $A$ is $BC$ and the side adjacent to $A$ is $CA.$
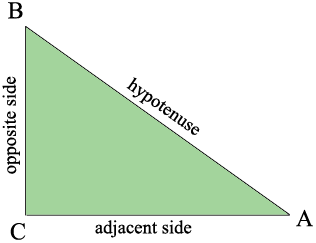
Suppose that measure of the angle at $A$ is $37^o .$ Suppose you also know that the length of $CA$ is $ 15$ centimeters then
\[\tan(37^o) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{|BC|}{|CA|} = \frac{|BC|}{15},\]
and hence
\[|BC| = 15 \times \tan(37^o).\]
Now it's time to use your calculator. Make sure it is set on degrees and input $\tan(37).$ My calculator gave me $\tan(37) = 0.7536$ and hence
\[|BC| = 15 \times 0.7536 = 11.3 \mbox{ centimeters.}\]
Write back if I haven't answered your question,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.