| |||
| Math Central | Quandaries & Queries |
|
Question from Anonymous, a student: An equilateral triangle with sides 6 inches is inscribed in a circle. What is the diameter of the circle? |
Hi,
By the symmetry in my diagram the measure of angle $BCA$ is $\frac{360}{3} = 120$ degrees. The sum of the measures of the angles of a triangle is $180^o$ and hence the measure of angle $CAB$ is $30^o$.
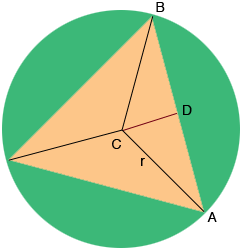
D is the midpoint of $BA$ and hence angle $ADC$ is a right angle. Do you see why? What trig function relates the measure of angle $CAD$ to the lengths of $CA$ and $AD?$
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.