Hi Brad,

Here is my sketch of your wall, not to scale.

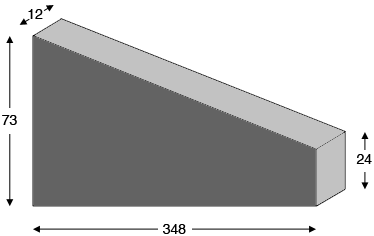
The volume of concrete needed is the area of the face of the wall times its thickness of 12 inches.

To find the area of the face of the wall I drew a horizontal line across the wall to divide the face into a rectangle and a triangle.

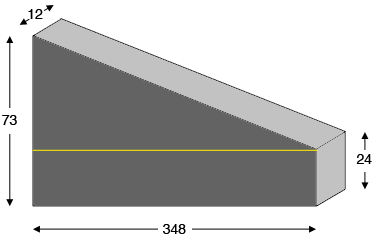
The rectangle has area $348 \times 24$ square inches and the triangle has base length $348$ inches and height $73 - 24 = 49$ inches. Hence the area of the triangle is $\large \frac12 \normalsize \times 348 \times 49$ square inches. Thus the area of the face is

\[\left( 348 \times 24 + \frac12 \times 348 \times 49 \right) \times 12 \mbox{ cubic inches.}\]

I expect you want the volume in cubic yards. Google will make this conversion for you. Type x cubic inches in cubic yards into the Google search window, where x is the volume in cubic inches, and Google will return the result in cubic yards.

Penny