Hi Cherrielyn,

I drew a circle of radius $r$ feet and an arc $A,$ subtended by an angle of $t^o$ at the center of the circle.

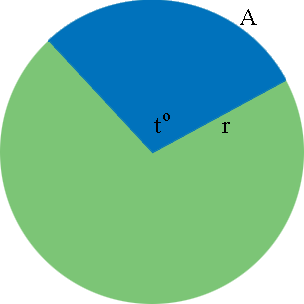
The circumference of the circle is $2 \pi \; r$ feet. The length of the arc $A$ is a fraction of the circumference and the angle of measure $t^o$ is a fraction of $360^o .$ By the symmetry of the circle you can see that the fractions are the same. For example if $t = 180$ then $t$ is half of $360$ and $A$ is half of the circumference. That is

\[A = \frac{180}{360} \times 2 \pi \; r = \frac{1}{2} \times 2 \pi \; r = \pi \; r.\]

Likewise if $t = 90$ then

\[A = \frac{90}{360} \times 2 \pi \; r = \frac{1}{4} \times 2 \pi \; r = \frac12 \pi \; r.\]

The same relationship is true regardless of the value of $t.$ That is in general

\[A = \frac{t}{360} \times 2 \pi \; r = \frac{t}{180} \times \pi \; r.\]

Your railroad track is made up of two arcs. Find the length of each arc and add them to determine the length of the track.

Penny