Hi Cierra,

I would experiment a little before doing any calculation. By experiment I mean to draw a scale diagram, I used 40 mm or the shorter of the two sides and 48 mm for the longer of the two sides. (My diagram below is not to scale.)

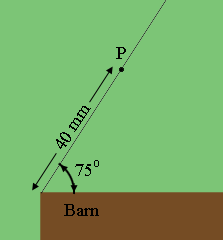
I put one vertex of the triangle at the north west corner of the barn and used a protractor to construct a $75^o$ angle at this point. I then measured 40 mm along the side of pen and placed a point $P$ there. Now take a compass, set the distance between the point and the pencil to 48 mm, set the point at $P$ and draw an arc that intersects the side of the barn at the point $Q.$ Join $P$ and $Q$ to obtain one option for the pen.

Draw a second diagram with $P$ 48 mm along the north west side of the pen. This time set the compass to 40 mm.

Now that you have all possible pen shapes you could place each of them at either end of the barn and with the $75^o$ angle at the corner or $Q$ at the corner.

For the possible lengths of the barn side of the pen I think you will need the Law of Sines and the Law of Cosines.

Penny