| |||
| Math Central | Quandaries & Queries |
|
Question from c.j, a student: what is the length of the radius of the LARGER cone(the LARGER cone has a slant height of 15) when the SMALLER cone has a radius of 8 and a slant height of 12ft ,please help. |
Hi,
I assume have a diagram that looks something like this.
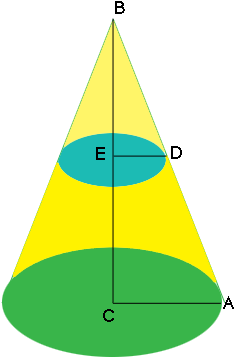
If so then the triangles $ABC$ and $DBE$ are similar and thus
\[\frac{|AB|}{|BC|} = \frac{|DB|}{|BE|}\]
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.