| |||
| Math Central | Quandaries & Queries |
|
Question from David: It is known that a fish in water looking up has a 97 degree "cone" of vision that sees "through" the surface of the water. If a fish lies 4 inches below the surface, the cone forms a window (circle) smaller than if a fish lies 8 inches below the surface. What is the ratio of inches of depth to the radius of the circle on the surface that is its visual window? |
Hi David,
I drew a rough diagram of what you describe.
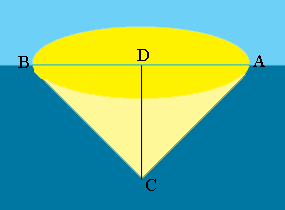
The measure of the angle $BCA$ is $97^o$ so the measure of the angle $DCA$ is half of that. $|DC|$ is the depth of the fish and $|AD|$ is the radius window. What trig function relates the measure of the angle $DCA$, and the side lengths $DC$ and $AD?$
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.