Henry,

Can you send me a link to John Lucas' web page so that I can see what this looks like?

Harley

Henry sent a photo

Harley wrote

Henry,

How many staves do you plan to use or maybe I should ask how wide will a stave be at the bottom?

Harley

Henry wrote back with more photos and some information from John Lucas

It's 17" wide and 49" tall at the top of the wood. It holds 3 rifles and 2 handguns. Made from Maple and Walnut.

Harley replied

I drew a picture of the bas of the lamp showing in dark brown the base of one stave (not to scale).

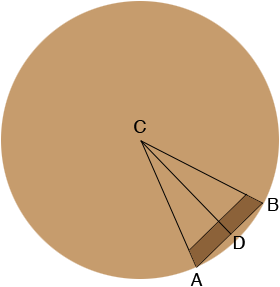
I am going to show you some general expressions so that you can change the dimensions if you choose and then do some calculations using the dimensions you supplied.

Suppose the radius of the base, $CB,$ is $R$ inches, the width of the stave, $AB,$ is $W$ inches and that there are $n$ staves. Since the $n$ staves are the angle $CBA$ has measure $\large \frac{360}{n}\normalsize \mbox{ degrees. }$

The line $CD$ bisects the angle $BCA$ and hence $D$ is the midpoint of $AB$ and the angle $CDB$ is a right angle. Thus

\[\sin\left( \frac{180}{n} \right) = \frac{W/2}{R}\]

and thus

\[W = 2 R \sin\left( \frac{180}{n} \right).\hspace{25 mm} (1)\]

If we use the data given, $R = \large \frac{17}{2}$ and $n = 16$ this gives $W = 17 \sin\left(\frac{180}{16}\right) = 3.32 \mbox{ inches.}$

Suppose the measure of the angle $DBA$ is $\theta$ degrees. Since the sum of the measures of the angles of a triangle is 180 degrees

\[\theta = 180 - 90 - \frac{180}{n} = 90 - \frac{180}{n} \mbox{ degrees.} \hspace{25 mm} (2)\]

Again if we take $n = 16$ then $\theta = 90 - \frac{180}{16} = 78.75$ degrees.

In the diagram od a stave below (again not to scale) I have extended the sides to meet at C.

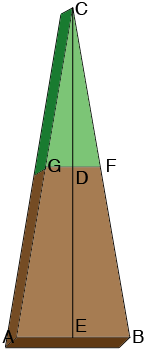
Suppose the height of the lamp is $h$ inches so in the diagram above The distance from $E$ to $D$D is $h$ inches. Suppose the width of the stave at the top, $GH,$ is $w$ and the height of the triangle $CAB$ is $H.$ Then since $CAB$ and $CGF$ are similar triangles

\[\frac{H}{W} = \frac{H - h}{w} \]

or

\[H = \frac{hW}{W-w}\hspace{25 mm} (3)\]

Since triangle $CEB$ is a right triangle

\[\tan\left(CEB\right) = \frac{H}{W/2}\]

and thus

\[CEB = \tan^{-1}\left(\frac{2H}{W}\right) \hspace{25 mm} (4)\]

I don't have a value for $w,$ the width at the top of the stave but once you decide what you want it to be you can use equation (3) to find $H$ and then use equation (4) to find the measure of the angle $CEB.$

Write back if you need any more help with this,
Harley