Hi,

It is difficult to give an intuitive answer to your question. The modern proof that the volume of a cone is $\frac13 \times \mbox{ area of the base} \times \mbox{ height}$ is by using calculus. You can take the essence of the calculus proof and present it without using calculus. That's what Dr. Rob did on the Math Forum site.

In fact the volume of a cone is $\frac13 \times \mbox{ area of the base} \times \mbox{ height}$ follows from a much more general result.

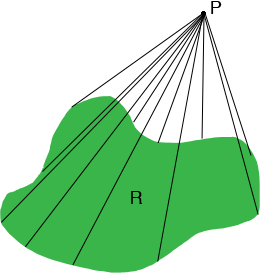
Suppose R is a region in the plane with an area and P is a point not in the plane, at a height h above the plane. Join each point on the boundry of R to P to form a "cone".

The volume of this "cone" is $\frac13 \times \mbox{ area of the base} \times \mbox{ height.}$

Penny