Hi James,

I'm going to write an expression for the area of the "cap" $ABED$ as the area of the sector $CABE$ minus the area of the triangle $CAE.$

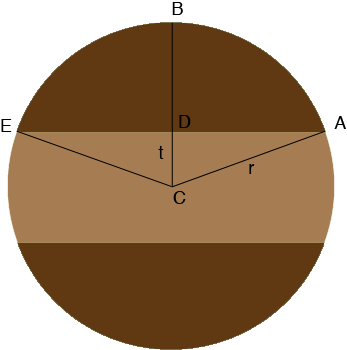
The area of a sector of a circle of radius $r$ is $\large \frac12 \normalsize r^2 \theta$ where $\theta$ is the central angle measured in radians. In this case the central angle is the angle $ECA$ which is twice the angle $DCA.$ Since triangle $ADC$ is a right triangle

\[\cos\left(\frac{\theta}{2}\right) = \frac{t}{r} \]

and hence

\[\frac{\theta}{2} = \cos^{-1}\left(\frac{t}{r}\right) \]

and thus the area of the sector $CABE$ is

\[r^2 \cos^{-1}\left(\frac{t}{r}\right).\]

Since triangle $ADC$ is a right triangle Pythagoras Theorem tell us that the length of $DA$ is $\sqrt{r^2 - t^2}$ and hence the area of the triangle $CAE$ is

\[t \sqrt{r^2 - t^2}\]

and thus the area of the cap $ABED$ is

\[r^2 \cos^{-1}\left(\frac{t}{r}\right) - t \sqrt{r^2 - t^2}\]

and hence the area of the light brown slice you want to remove from the cake is

\[\pi \; r^2 - 2 r^2 \cos^{-1}\left(\frac{t}{r}\right) + 2 t \sqrt{r^2 - t^2}.\]

In the situation you describe with a 12 inch diameter cake from which you want to remove a centre slice with surface area one eighth of the cake you have

\[\frac18 \pi \; \times 36 = \pi \; \times 36 - 2 \times 36 \; \cos^{-1}\left(\frac{t}{6}\right) + 2 t \sqrt{36 - t^2}\]

and you want to solve for $t.$

This expression can be simplified somewhat to give the equation

\[ \frac{63}{4} \pi - 36 \; \cos^{-1}\left(\frac{t}{6}\right) + t \sqrt{36 - t^2}= 0\]

but unfortunately this equation can't be solved for $t$ to give the "simple" solution you desire.

Harley