| |||
| Math Central | Quandaries & Queries |
|
Question from jeffrey, a student: the towers of a parabolic suspension bridges 200 meter long are 40 meter high and the lowest point of the cable is 10 meter above the roadway.Find the vertical distance from the roadway to the cable at 50 meter from the center. |
Hi Jeffrey,
I drew a diagram on the Cartesian plane with the origin 10 m below the lowest point of the cable.
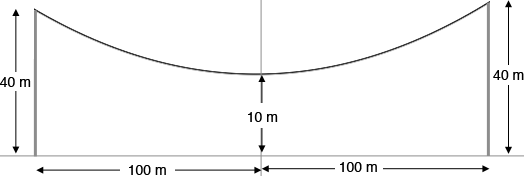
Since the cable forms a parabola its equation is $y = a x^2 + b x + c$ for some numbers $a, b$ and $c.$
Since you know $(0, 10)$ is on the graph of the parabola you have $10 = a \times 0^2 + b \times 0 + c$ you know that $c = 10.$
You also know that $(100,40)$ and $(-100, 40)$ are on the graph so substitution gives you two equations to solve for $a$ and $b.$
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.