Hi,

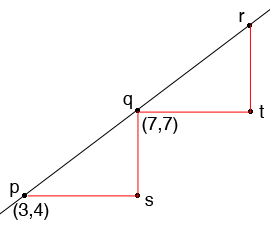
What are the coordinates of $s?$

Triangle $sqp$ is a right triangle. What does Pythagoras theorem tell you is the length of the line segment $pq?$

The distance from $p$ to $r$ is 10. What is the distance from $q$ to $r?$

What are the coordinates of $t$ and $r?$

Penny

There are of course two answers, depending on whether Q lies between P and R (which is suggested but not, in my opinion, actually stated.)

It's easier that it looks. First draw a reasonably accurate sketch.

Now use Pythagoras' Theorem to find the distance |PQ|.

So where would R be?

(This depends on a small coincidence that makes the numbers come out nicely, but don't be ashamed to use it; these appear in mathematical "real life" too. To solve a more general problem, you would compute the "direction cosines"

\[c_x = (Q_x-P_x)/|Q-P|\]
\[c_y = (Q_y=P_y)/|Q-P|\]

These are the run and rise of a unit vector in this direction. They are always between -1 and 1, and the sum of their squares is always 1. Multiply by 10 to get the actual run and rise, and add to the coordinates of P to get those of R:

\[R_x = P_x + 10 c_x\]
\[R_y = P_y + 10 c_y\]

)

Good Hunting!
RD