| |||
| Math Central | Quandaries & Queries |
|
Question from Jim: A recent puzzle ' find the length of a string around 3 touching 1 meter diameter circles ' gave this answer : the string touches 120° (or pi/3 meters) of each circle. Then 3(1+pi/3) = 3+pi meters is the required length. I do not see how it was determined that the string touches 120° or pi/3 meters? |
Hi Jim,
In my diagram Q i the centre of the circle that is tangent to AB and AC and R and P are the points of tangency. Hence angles QRB and BPQ are right angles. The hypotenuse and one leg of the right triangle QRB and the hypotenuse and one leg of the right triangle QBP are congruent and hence the triangles QRB and QBP are congruent.
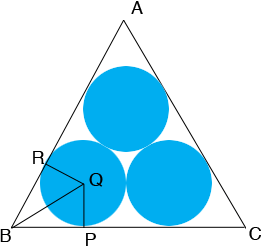
Since triangles QRB and QBP are congruent angles RBQ and QBP are congruent. Since the measure of the angle RBP is 60 degrees the angles RBQ and QBP each have measure 30 degrees. Since the sum of the measures of the interior angles of a triangle is 180 degrees angles BQR and PQB each have measures 60 degrees. Thus the measure of the angle BQR is 180 degrees.
Since the string wraps around the circle centred at Q and is in contact with the circle along the arc from R to P the length of this portion of the string is pi/3 metres.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.