Hi Josh,

Here is my diagram of your truncated cone, the diagram is certainly not to scale. I also drew it upside down to the way you described it.

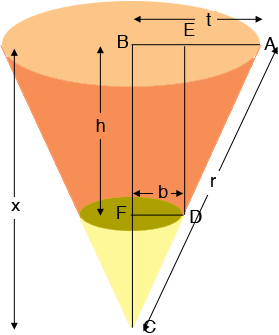
I extended the sides of the truncated cone to meet at $C$ and form a full cone. In your situation the diameter at the top is $D = 18"$ and the diameter at the bottom $d = 15.25"$ and $h = 20".$ Thus $t = 9"$ and $b = 7.625".$ Triangles $ABC$ and $DFC$ are similar so

\[\frac{x}{t} = \frac{h}{t - b}\]

and hence

\[x = \frac{ht}{t - b}.\]

The slant height $|CA| = r $ is given by Pythagoras Theorem as

\[r = \sqrt{\left( \frac{ht}{t - b} \right)^2 + t^2}\]

Similarly the slant height $|DA|$ of the truncated cone is given by

\[s = |DA| = \sqrt{(t - b)^2 + h^2}.\]

Now slice the cone from $A$ to $C$ and lie it flat.

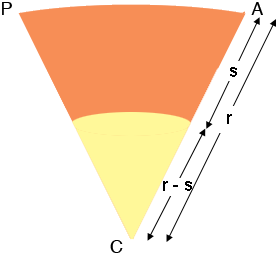
The length of the arc from $A$ to $P$ is the circumference of the large end of the truncated cone so the length of the arc from $A$ to $P$ is $2 \pi \; t$ units. The angle $ACP$ is a fraction of the $360^o$ that makes up the circle. That fraction is

\[\frac{2 \pi \; t}{2 \pi \; r} \times 360^o = \frac{t}{r} \times 360^o\]

The construction is then to draw two circles with radii $r$ units, in your case inches, and the other with radius $r - s$ units, each with the same center P. Cut out the wedge $ACP$ with center angle measure of $\frac{t}{r} \times 360$ degrees. Roll up the wedge to form the truncated cone. I don't know what material you are using but I would do it on scrap material first.

Penny

In March of 2014 Don Nevin, a retired mathematician from Vermont Technical College, sent us an Excel spreadsheet which can be used to calculate the dimensions required to produce a flat template for a truncated cone. Don kindly gave us permission to make his spreadsheet available to Math Central users. You can download his spreadsheet here. Notice that in Penny's response above the wedge $ACP$ is the piece to be rolled up to form the truncated cone. In Don's spreadsheet the angle $\Theta$ is the central angle of the sector to be removed so that the remainder is to be rolled up to form truncated cone. Thus $\frac{t}{r} \times 360 = 360 - \Theta.$

Thanks Don.