| |||
| Math Central | Quandaries & Queries |
|
Question from Lexie, a student: Determine the area that is bounded by the following curve and the x-axis on the interval below. (Round your answer to three decimal places) y=x^(2)-4, -5 ≤ x ≤ 0 The answer is 32.333 but I have no idea how to get there. |
Hi Lexie,
$y = 0$ when $x = \pm 2$ and $x = -2$ is in the interval $-5 \leq x \leq0$ and hence I needed to see a graph of the function. Here is my graph and you can see that for $-5 \leq x \leq -2$ the graph is above the X-axis and for $-2 \leq x \leq 0$ the graph is below the X-axis.
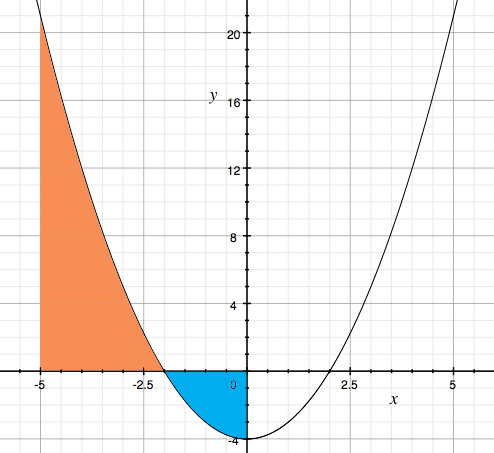
Thus if you integrate $y = x^2 - 4$ from -5 to -2 you will get the area I shaded orange in the diagram. If you integrate $y = x^2 - 4$ from -2 to 0 you will get minus the area I shaded blue. Thus the area you want is the integral of $y = x^2 - 4$ from -5 to -2 MINUS the integral of $y = x^2 - 4$ from -2 to 0.
Write back if you have trouble finishing the problem.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.